回答

HashMap 的容量被设计为 2^n，主要有如下几个优势：

位运算效率：与使用取模（%）操作相比，使用位运算来计算索引位置更加高效。当容量是 2^n 时，计算索引的公式可以从 (hash % capacity) 简化为 (hash & (capacity - 1))，这个操作仅涉及位与运算，比取模操作更快。
元素分布更加均匀：利用哈希码的低位直接作为数组索引，确保了元素能够被均匀分布在整个 HashMap 中，从而在理想情况下减少了哈希冲突，提高了 HashMap 的整体性能。
扩容性能更佳：HashMap 的初始容量是2^n，扩容也是以 2 倍的形式进行扩容，这样在进行扩容重新分布元素时，我们只需要对参与计算的最高位进行检测，如果为 1 就向高位移动 2^(n-1) 位，为 0 就保持不动。无需重新计算所有 key 的 hash 值再来重新分布。

详解

HashMap 的默认容量是 1 << 4，也就是2^4，也就是16。当我们指定容量大小的时候，如果这个值不是 2^n，HashMap 就会将其处理为 2^n。

    public HashMap(int initialCapacity) {
        this(initialCapacity, DEFAULT_LOAD_FACTOR);
    }
    
    public HashMap(int initialCapacity, float loadFactor) {
        // 处理初始容量
        this.threshold = tableSizeFor(initialCapacity);
    }

使用 tableSizeFor() 对初始容量进行处理：

    static final int tableSizeFor(int cap) {
        int n = cap - 1;
        n |= n >>> 1;
        n |= n >>> 2;
        n |= n >>> 4;
        n |= n >>> 8;
        n |= n >>> 16;
        return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
    }

这个方法用于计算给定容量 cap 最接近的、大于或等于该值的 2^n 的数。可能有小伙伴看到这个方法就懵逼了，大明哥用 21 来详细介绍下，它是如何处理得到 32 的。

int n = cap - 1：这一步的目的是为了简化后面的位操作n = 21 - 1 = 20，二进制为：10100；
n |= n >>> 1;
- 右移一位并进行位或运算，目的是把最高位的 1 右边的第一个位也设置为 1。
- n >>> 1 右移一位得到 01010 ，然后与 10100 位或运算，得到 11110，为 30。
n |= n >>> 2;
- n >>> 2 右移两位得到 00111，然后与 11110 位或运算，得到 11111，为 32。
- 由于此时 n 已经全部都是 1 了，所以再进行右移和位或操作，n 保持不变，即 11111，为 32。

然后重复这个过程，分别是 n >>> 4、n >>> 8、n >>> 16。每一步都将前面步骤中生成的 1 向右扩散，确保从最初的最高位 1 到最低位，所有位都被设置为 1。

为什么 HashMap 要进行这样的操作呢？主要有如下三个原因：

位运算效率：与使用取模（%）操作相比，使用位运算来计算索引位置更加高效。当容量是 2^n 时，计算索引的公式可以从 (hash % capacity) 简化为 (hash & (capacity - 1))，这个操作仅涉及位与运算，比取模操作更快。
元素分布更加均匀：利用哈希码的低位直接作为数组索引，确保了元素能够被均匀分布在整个 HashMap 中，从而在理想情况下减少了哈希冲突，提高了 HashMap 的整体性能。
扩容性能更佳：HashMap 的初始容量是2^n，扩容也是以 2 倍的形式进行扩容，这样在进行扩容 hash 重分布时，只有两种情况：要么保持不变，要么在原索引位置上 + n，性能比打散重新再分布性能更好。

位运算效率

因为位运算仅仅只涉及到简单的二进制位操作，而不需要复杂的算术计算。而取模运算涉及到除法运算，除法运算确是 CPU 中相对复杂和耗时的操作之一，因为它涉及到多步骤的算术计算。

所以，相比于位运算，取模运算需要更多的CPU周期来完成。

如果我们不将 HashMap 的容量约定为 2^n，是无法将 % 运算转换为 & 运算的。而x % 2^n = x & (2^ - 1)，可以把 % 运算转换为 & 运算，这样性能就大大提高了。

那为什么 x % 2^n = x & (2^ - 1)呢？

当我们用一个数 x 去取模 2^n 时，实际上是在找出 x 中能够被 2^n 整除的最大部分的余数。在二进制中，2^n 总是像 100...0（后面跟着 n 个 0）。因此，x 除以 2^n 的余数只与 x 的二进制表示中的最低 n 位有关，这正是按位与操作 x & (2^n - 1) 所保留的部分。

看不懂？举个例子，假设 n = 4，x = 25。25 % 2^4 它是等于 25 / 2^4 的余数，即 25 >> 4（11001 右移 4 位），而被移除到的部分（4 位 1001）就是我们的余数，即x 除以 2^n 的余数只与 x 的二进制表示中的最低 n 位有关。而 25 & （16 -1） = 11001 & 1111 = 1001。

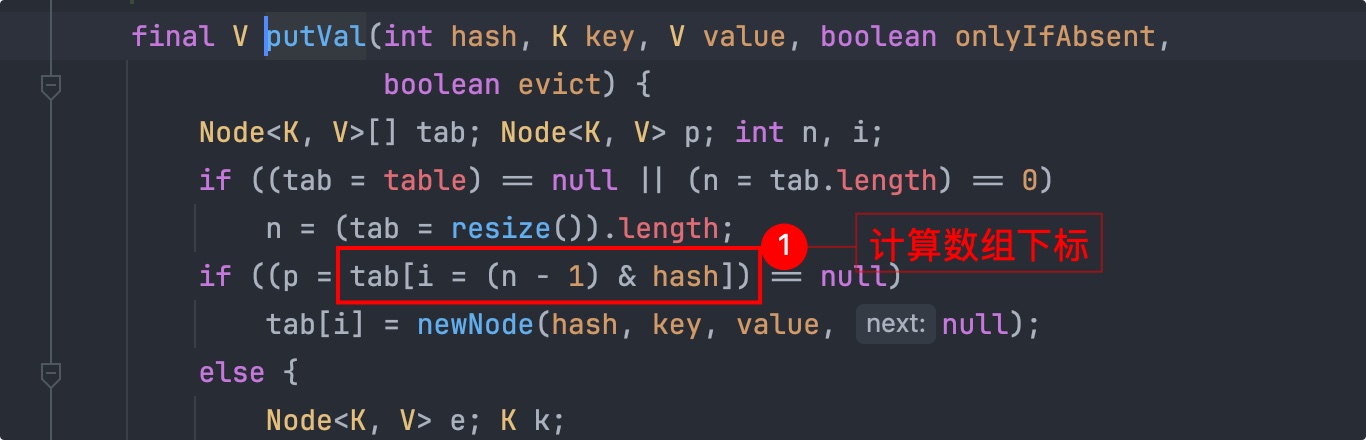
所以你会看到 HashMap 在获取数组下标时采用的方式就是位运算，例如 put()：

分布更加均匀

我们先写个简单的案例测试下，我们新建一个 Student 对象，利用它的 hashcode 分别与 12、16 、 25 、32，按照 HashMap 那样定位 index 的方式来计算值（公式：(table.length - 1) & (key.hashCode ^ (key.hashCode >> 16))），然后放入到 HashMap 中去，看看 HashMap 的结果就可以知道分布情况了。

Student 对象

@Data
@AllArgsConstructor
public class Student{
    private String name;

    private Integer age;
}

测试程序：

public class HashMapTest {
    public static void main(String[] args) {
        Map<Integer,Integer> resultMap = new HashMap<>();
        int k = 16;   // 修改这个
        // 循环创建 500 个对象
        for (int i = 0; i < 500 ; i++) {
            Student student = new Student("skjava-" + i,i);
            int h = student.hashCode();
            int hash1 = h ^ (h>>>16);
            int hash = (k - 1) & hash1;
            if (resultMap.containsKey(hash)) {
                int count = resultMap.get(hash);
                resultMap.put(hash,count + 1);
            } else {
                resultMap.put(hash,1);
            }
        }

        resultMap.forEach((key,value) -> System.out.println("key:" + key + "    value:" + value));
    }
}

最终得到的结果分布图如下：

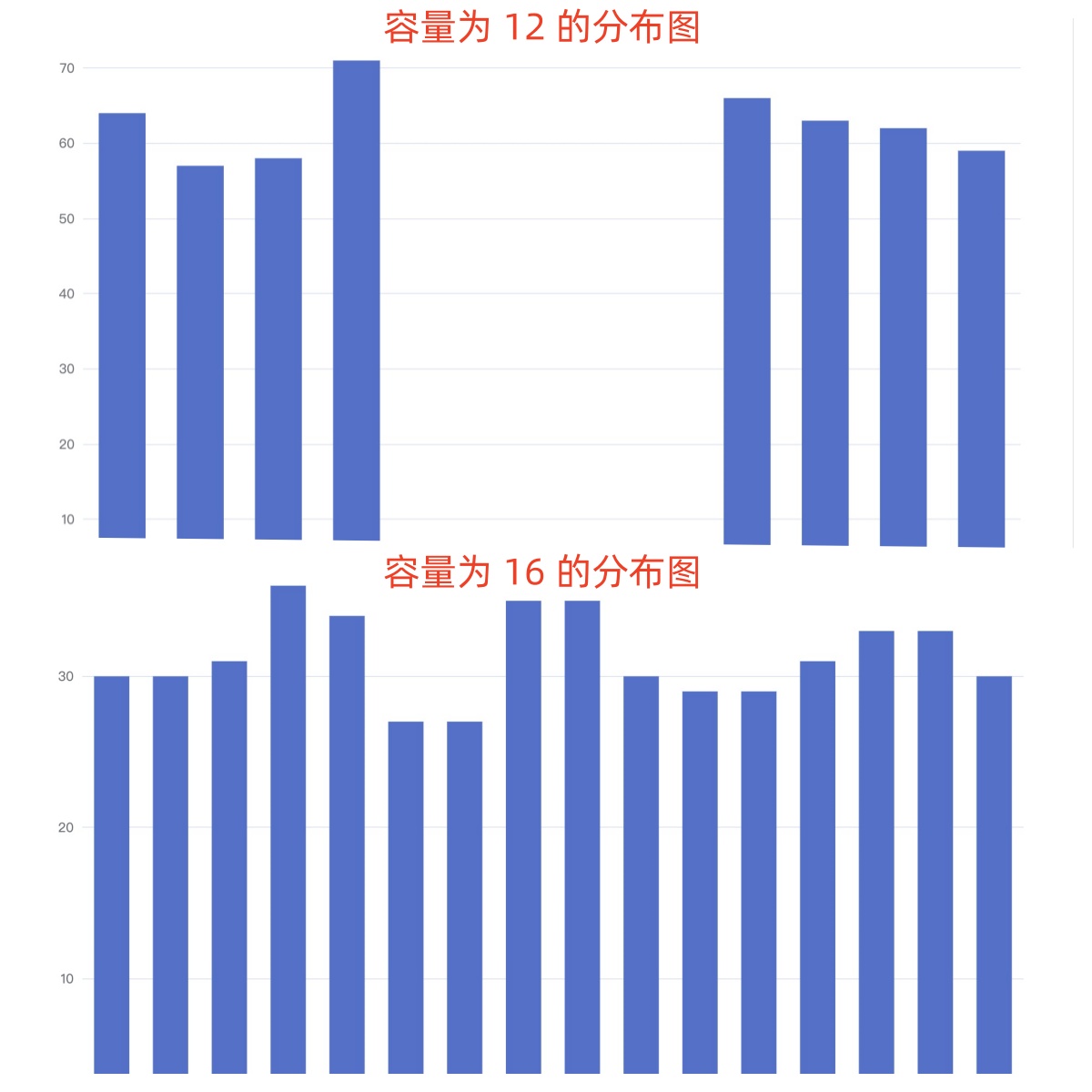
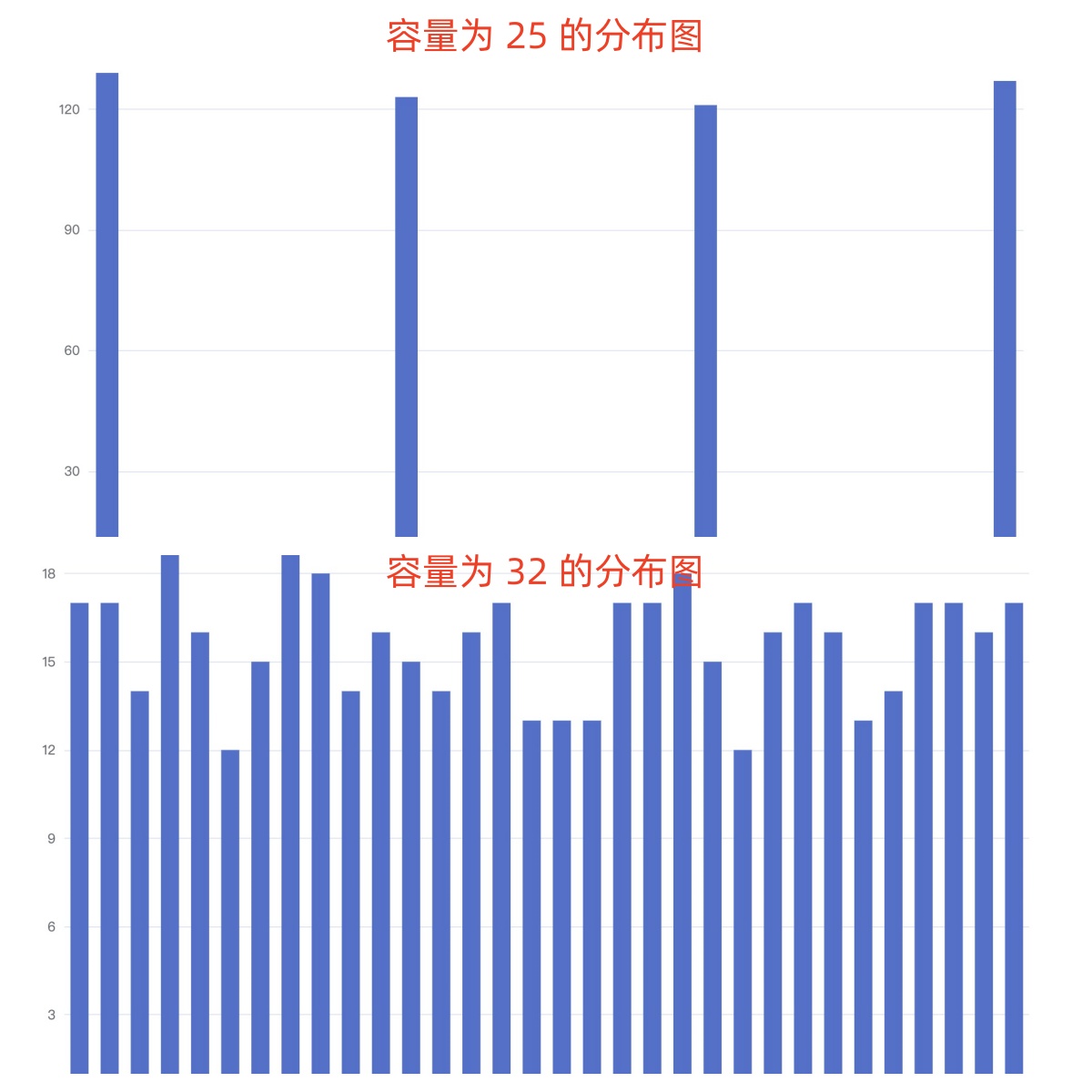
从上图可以看出只有容量为 16 和 32 的分布是均匀的，而 12 和 25 分布都极其不均匀。为什么会出现这种情况？我们以 s 的 hash （115 = 1110011）值为例。最接近的 127，则 "s".hashCode() & (127 - 1) 如下图：

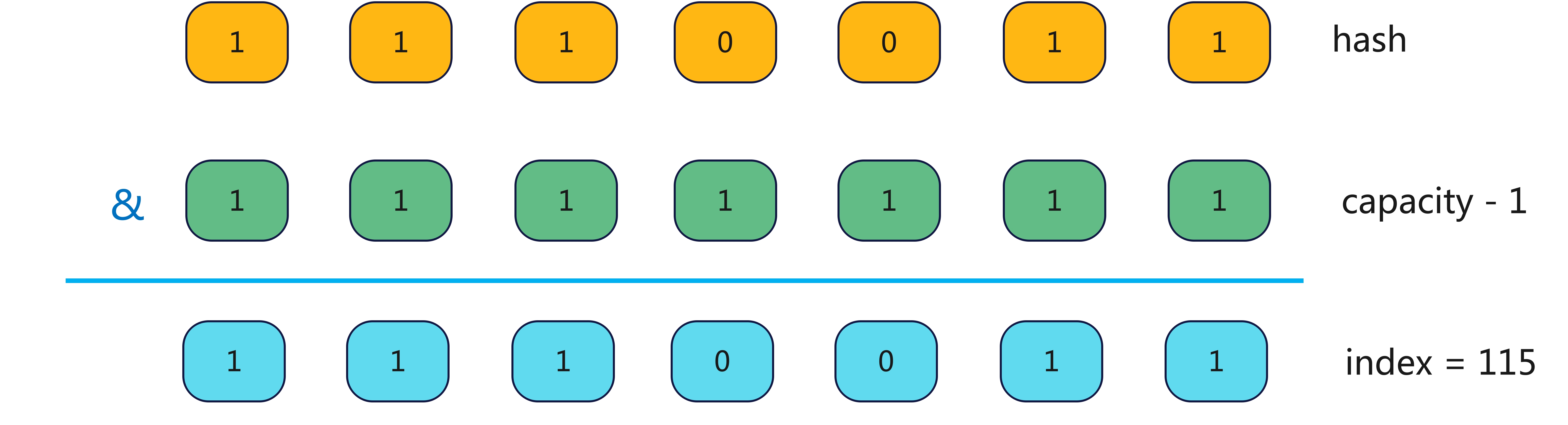
那如果 capacity 为106 呢？

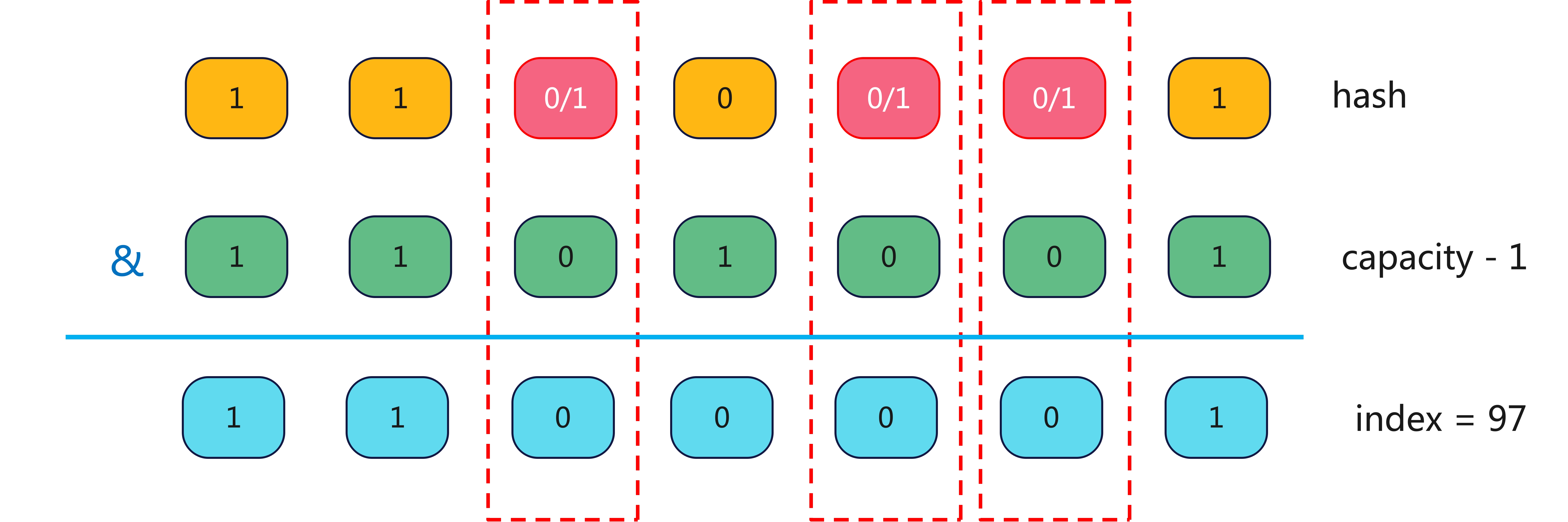
你会发现标红色虚线部分，无论是 0 还是 1 产生的结果都是一样的，所以如果 capacity 为 106，则它产生的 hash 冲突比 127 大的多。

所以，容量为 2^n ，它能够利用哈希码的低位直接作为数组索引，确保了元素能够被均匀分布在整个 HashMap 中，从而在理想情况下减少了哈希冲突。

扩容性能更佳

当 HashMap 的容量超过阈值后，就会进行扩容操作，扩容就会设计到 hash 重分布的。而重分布的过程是重新计算所有 key 的 hash 值，然后再重新分布，这个过程非常繁重且性能极低。如果我们将 HashMap 的容量保持为 2^n，就避免了这个过程，会变得非常简单而又高效。

加入我们有这样一批 key：s、i、k、e、c、o、m，为了更好地演示，HashMap 的初始容量为8，所以数据分布如下：

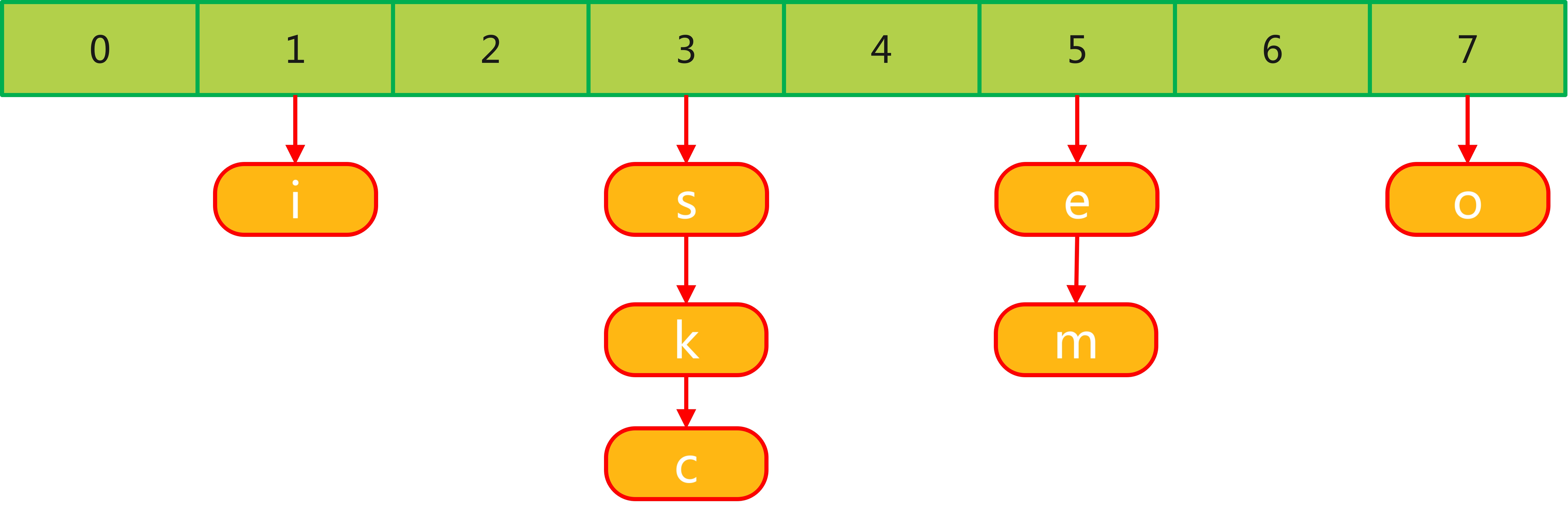
现在我们扩容到 16 去，index = hash & (16-1)，上面 7 个字母调整位置如表：

key	key 二进制值	key ^ (16-1)	原始位置	扩容 16后位置	结果
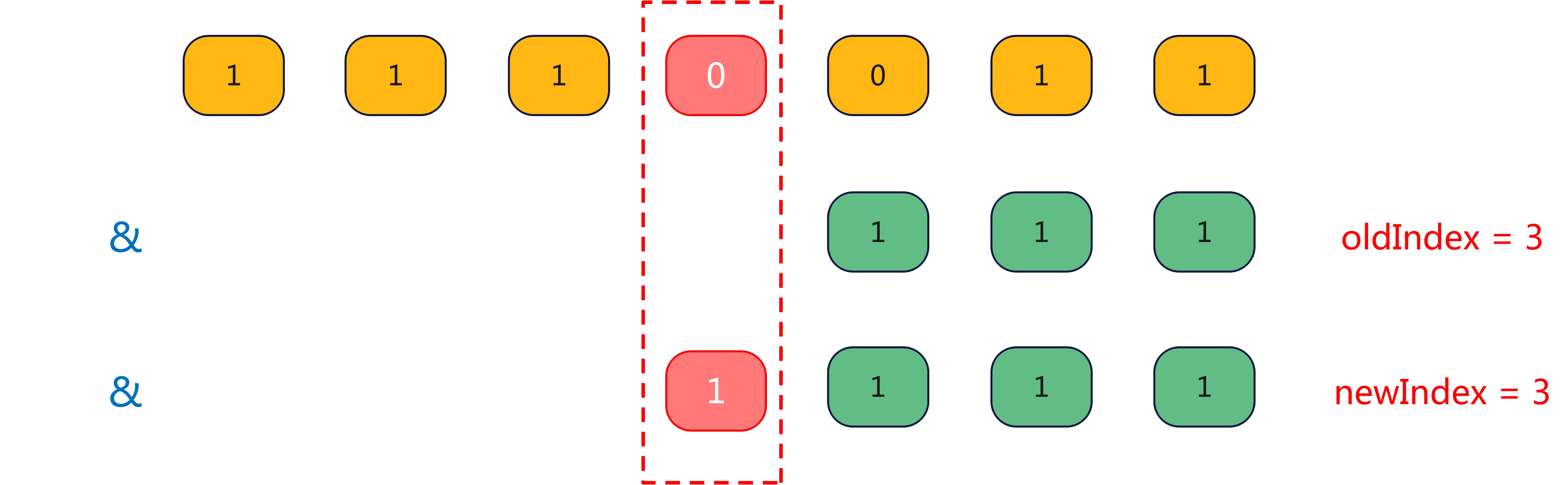
s	1110011	0011	3	3	不动
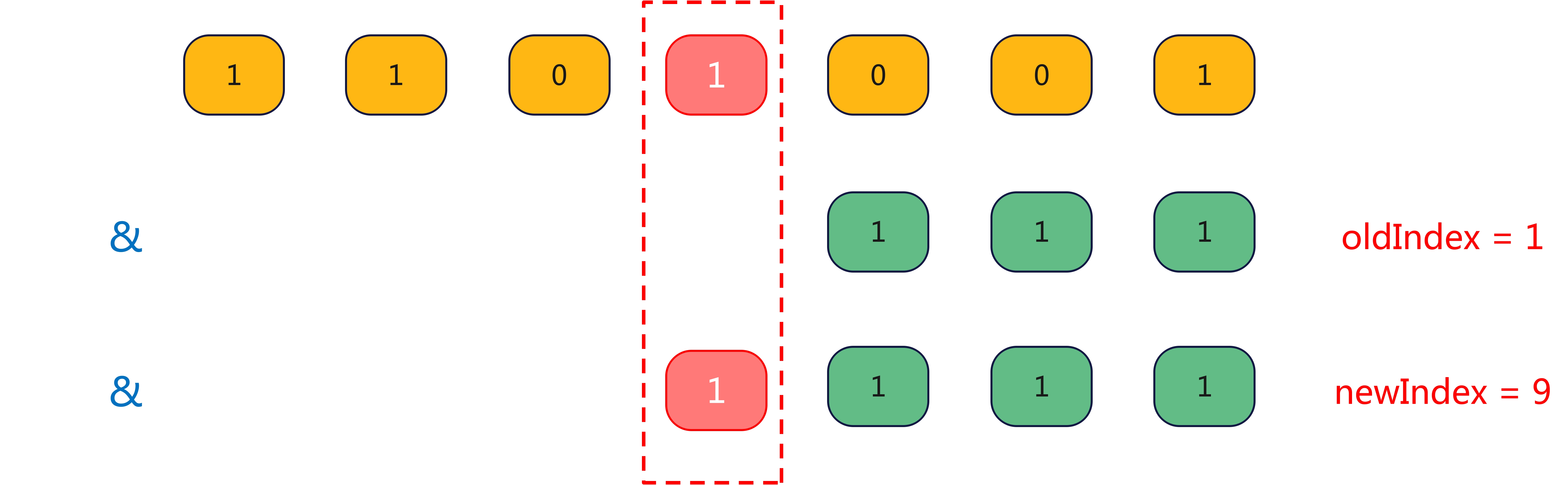
i	1101001	1001	1	9	移动 8 位
k	1101011	1011	3	11	移动 8 位
e	1100101	0101	5	5	不动
c	1100011	0011	3	3	不动
o	1101111	1111	7	15	移动 8 位
m	1101101	1101	5	13	移动 8 位

看不明白？下图 s 的 index 变化图：

再看 i 的 index 变化图：

从上图 s 和 i 的变化图中可以看出，HashMap 的扩容是否需要移位，由扩容后 key 的 hashcode 参与计算的最高位是否 1 所决定，并且移动的方向只有一个，即向高位移动。因此，在扩容后，我们不需要对每个 key 都进行计算然后来重新分配位置，我们只需要对最高位进行检测，如果为 1 就向高位移动 2^(n-1) 位，为 0 就保持不动，从而优化了性能。

Java 面试宝典是大明哥全力打造的 Java 精品面试题，它是一份靠谱、强大、详细、经典的 Java 后端面试宝典。它不仅仅只是一道道面试题，而是一套完整的 Java 知识体系，一套你 Java 知识点的扫盲贴。

它的内容包括：

大厂真题：Java 面试宝典里面的题目都是最近几年的高频的大厂面试真题。
原创内容：Java 面试宝典内容全部都是大明哥原创，内容全面且通俗易懂，回答部分可以直接作为面试回答内容。
持续更新：一次购买，永久有效。大明哥会持续更新 3+ 年，累计更新 1000+，宝典会不断迭代更新，保证最新、最全面。
覆盖全面：本宝典累计更新 1000+，从 Java 入门到 Java 架构的高频面试题，实现 360° 全覆盖。
不止面试：内容包含面试题解析、内容详解、知识扩展，它不仅仅只是一份面试题，更是一套完整的 Java 知识体系。
宝典详情：https://www.yuque.com/chenssy/sike-java/xvlo920axlp7sf4k
宝典总览：https://www.yuque.com/chenssy/sike-java/yogsehzntzgp4ly1
宝典进展：https://www.yuque.com/chenssy/sike-java/en9ned7loo47z5aw

目前 Java 面试宝典累计更新 400+ 道，总字数 42w+。大明哥还在持续更新中，下图是大明哥在 2024-12 月份的更新情况：

想了解详情的小伙伴，扫描下面二维码加大明哥微信【daming091】咨询

同时，大明哥也整理一套目前市面最常见的热点面试题。微信搜[大明哥聊 Java]或扫描下方二维码关注大明哥的原创公众号[大明哥聊 Java] ，回复【面试题】即可免费领取。

阅读全文

Java 面试宝典：HashMap的容量为什么一定是2^n？

回答

详解

位运算效率

分布更加均匀

扩容性能更佳